Hay cosas que uno da por sentado en la vida y que, pensando un poco simplemente no tienen sentido. Me pasó con el béisbol. Me parece increíble que el deporte sea posible. Pensemos en la disposición: una persona batea una pelota que va muy rápido y tiene que ponerla dentro de un campo complicado. Hay 9 personas igualmente espaciadas en el campo esperando a que llegue la pelota, 7 más el pitcher y catcher. Si alguien la agarra en el aire el bateador queda fuera. Si llega al piso y se agarra la pelota y se lanza, otra vez muy rápido, a primera base, el bateador queda fuera. Todo está tan bien esquematizado que cualquier cosa que pase se puede escribir en una tabla.
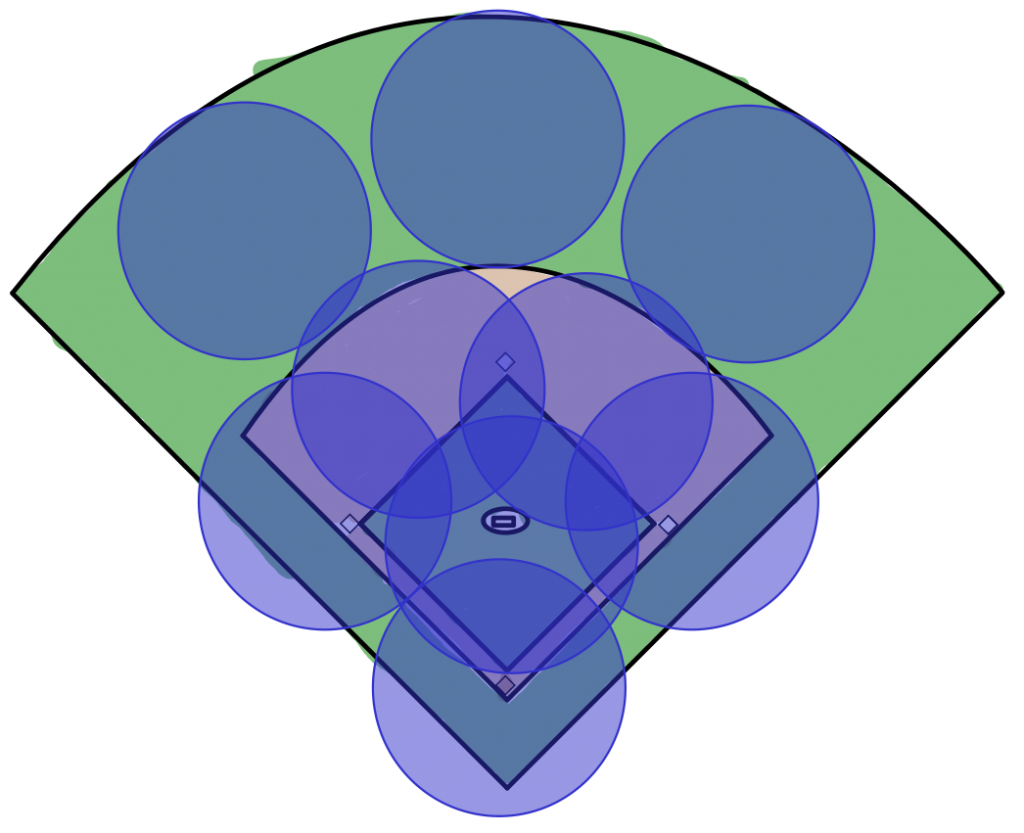
Parece, a priori, que la pelota llegará a cualquiera de ellos en casi cualquier forma que se pegue con el bat y que no salga del campo, lo que significaría un foul. Claro, ésta es una perspectiva desde arriba, pensando a las personas en el campo como atractores, que pueden moverse algo alrededor. Es decir, cada jugador defendiendo tiene cierto campo de acción para agarrar la pelota. En la imagen anterior se ve que cada jugador en el campo lleva una esfera alrededor que es el área que abarca. Mi problema entonces es que es una estructura rígida, no se ve por dónde pueda haber invención. ¿Dónde queda el juego?
Pensemos por ejemplo, en el fútbol. El arquero lanza la pelota a un jugador y este la controla y llega algún jugador del equipo contrario para quitársela. Hay demasiadas posibilidades para el jugador original, pasarla a un compañero, hacer fintas, ir más rápido. El juego en sí es muy abierto. No queda la imagen de una estructura rígida como en el béisbol. El juego es invención todo el tiempo, es propuesta, es reacción. Hay aspectos locales así como globales que tomar en cuenta, en fin, casi parece caótico en comparación.
Posiblemente sea que no entiendo del todo el tema y que la imagen como atractores (puntos que atraen la pelota) en el béisbol no sea del todo correcta en la práctica. Lo que puede pasar es que haya errores humanos que dejen pasar la pelota por en medio. Pero se juega profesionalmente y los jugadores entrenan mucho así que confiar en un error no es una estrategia ganadora, creo yo. Mi conclusión es que para que el deporte sea posible hay que abandonar la imagen expuesta previamente del juego. Se buscan los espacios vacíos entre los jugadores por dónde pasar la pelota, se busca siempre el desequilibrio de la estructura rígida. Se busca lo sutil. Para que puedan haber jugadas hay que perturbar lo suficiente a la estructura. Pero la forma de desequilibrio es con una pelota pequeña que tiene que meterse con esfuerzo a la superestructura. Y aún así se juegan temporadas y series mundiales.
Personalmente me recuerda al teorema de Knill-Gottesman en cómputo cuántico. Dicho teorema dice que si nos restringimos a un conjunto de operaciones cuánticas bien estudiadas que llamamos el grupo de Clifford, no sirve de nada hacer cómputo cuántico, ya que todas éstas operaciones y el resultado de las mismas se pueden simular eficientemente con una computadora clásica. El punto aquí es que existe un formalismo matemático para expresar estados cuánticos llamado formalismo de estabilizadores. Éste formalismo consiste en las compuertas cuánticas de Pauli para n qubits, compuertas de Hadamard y compuertas CNOT. El teorema parte de n estados en el estado 0 en la base computacional. Dicho grupo genera una variedad de estados grande y con entrelazamiento, da la impresión que no debería ser posible hacer computación cuántica que no sea clásica. Así que bueno, ¿Dónde queda el juego de la computación cuántica? Pues el juego está en la sutileza. Hay que ir fuera del grupo de Clifford. El símil con el béisbol surge en la imagen mental del teorema. Si se tienen recursos fuera de los antes mencionados se puede ir fuera del caso de Knill-Gottesman. Lo que se necesitan son estados que tengan cierta fase entre el 0 y el 1 en la base computacional. Se demuestra en un artículo por Bravyi y Kitaev que las operaciones del grupo de Clifford más la preparación de estados mágicos son suficientes para la computación cuántica universal.
Dichos estados mágicos que se agregan están en medio del campo explorado por el grupo de Clifford con los estados iniciales escogidos. A los estados cuánticos que no se llegan con el grupo de Clifford se les llama estados mágicos. Así es, la magia está en lo sutil, tanto en el béisbol como en cómputo cuántico.
Leave a Reply